In a previous post I looked at floating-point compression, and it generated quite a lot of interest on Twitter, with lots of people suggesting things. So I haven’t tried them all (only the first few that people suggested), but I thought I’d present the results I did try. First, the chart!

A chart of different floating-point compression methods. I’ll talk in detail further on, so the chart isn’t a necessity (more a pretty picture to make the post nicer!)

There was three different approaches that I looked at with this chart.

zfp⌗

One thing that was suggested was zfp which claims to compress floating-points really well. I really disliked the API to get this to work - really hard to use. Also it doesn’t have a streaming API, so you need to declare up front how many floats are in it. Given that I’m compressing 16GB worth of floating point numbers, I didn’t want to load up all 16GB of them at one go! So the approach I used was to batch them into 128MB regions, and compress these. Overall zfp achieves a 1.8x compression ratio against the raw data - which is 4x worse than the best compression we’ve achieved.

If we look at the compression ratio of each individual chunk in the chart below, we can see where we are losing out:

A chart of the compression ratio for each zfp chunk)

As we can see in the chart, the compression ratio of zfp is really good for the densely populated [0..1] range of floating-point numbers - getting a 6x compression ratio. It’s pretty terrible for the higher numbers though, hovering around 1.03x on average. Meaning basically no compression here at all. The higher inputs to cos will result in vastly different outputs, so its no suprising that the compression is worse up there.

fpzip⌗

Another was fpzip. Similarly to zfp above, there is no streaming API and I thus need to batch the input data. I choose the same chunk size of 128MB.

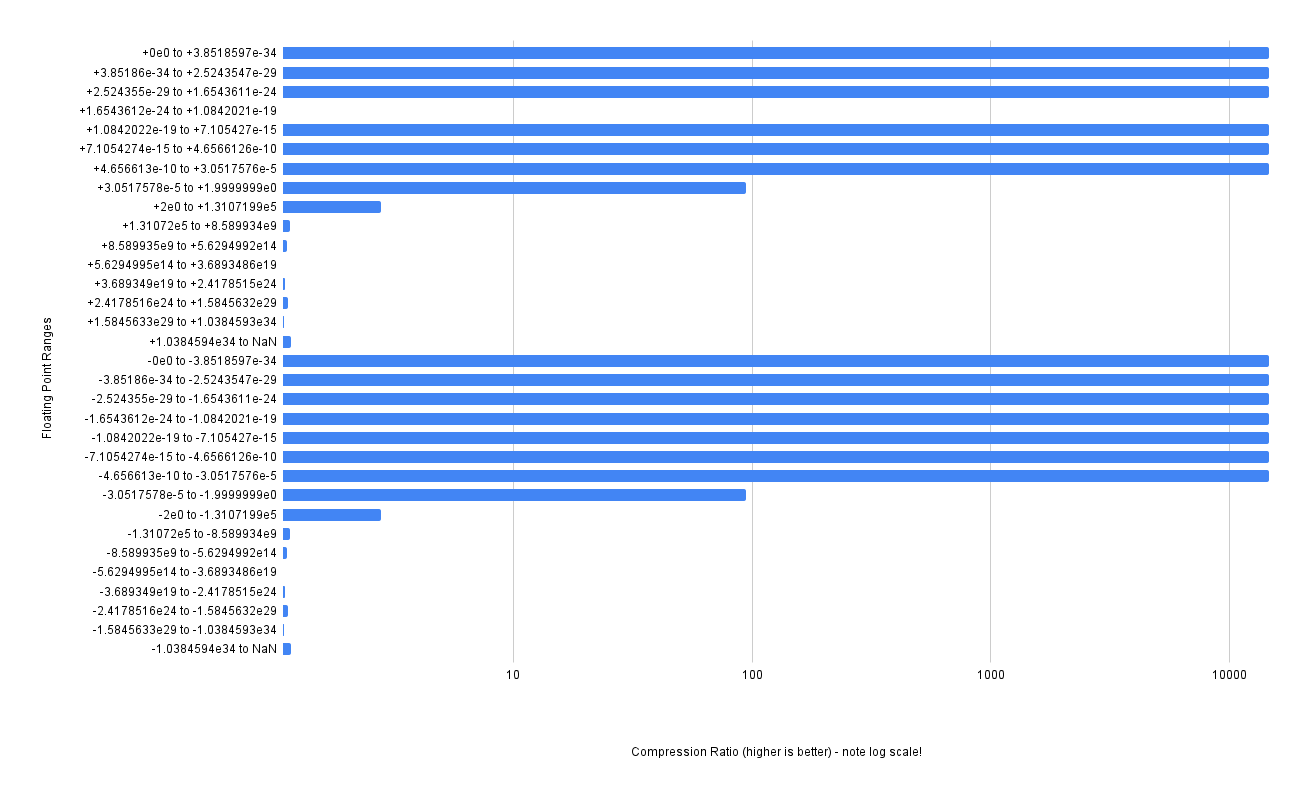
A chart of the compression ratio for each fpzip chunk in log scale)

Firstly - note the log scale for the chart. That’s because fpzip achieves a much much higher compression ratio for the numbers in the [0..1] range of floating point (almost a 14000x compression ratio, nice!). But it still suffers badly when the outputs from cos get wildly different - hovering around 1.09x on average. The compression ratio is better than zfp, with a 2.43x compression ratio overall compared to the raw data size, but it is still 2.98x worse than the best compression we have achieved.

Per-Bit Compression⌗

The best approach suggested was what if instead of doing a single zstd for the entire data stream, what if we do 32 zstd compressions, one for each bit of each float in the input stream? The general idea from people who proposed this approach was that so many of the bits would be consistent across subsequent output numbers, zstd would be much better at considering each bit separately.

This turned out to be the best approach I tested - zstd at compression level 10 was 2.9x more compressed doing per-bit compressed streams, and at compression level 21 it is 1.33x more compressed. Pretty cool!

Strangely xor’ing the previous with the current and then doing the per-bit calculation resulted in a worse zstd compression, but delta-encoding the previous with the current gave us a slightly higher compression ratio.

Also of note - doing delta-encoding with the per-bit zfp compression at zstd level 10 was 1.06x more compressed than doing the next best full-stream compression of xor’ing and zstd at compression level 21. This is interesting because compressing at level 10 was many many times faster to compute than using level 21.

Other Approaches⌗

There are for sure other approaches we could use here. Using the cos identity cos(x) = cos(-x) would cut the encoding range in half (as long as we correctly sign any NaNs produced). We could use a bit precise Payne-Hanek reduction so that we store only the [0..2π]range in the table. Food for thought (but I think I’ve scratched my itch with this problem for now!).